https://www.youtube.com/watch?v=tZu4x5825LI
내비게이션은 어떤 원리로 최단거리를 추천해줄까?
궁금하다면 다익스트라 알고리즘을 알아보자!
다익스트라(Dijkstar) 알고리즘은 그래프의 한 정점에서 모든 정점까지의 최단거리를 구하는 최단 경로 문제 알고리즘입니다.
- 음수 간선이 없는 경우 사용할 수 있고, 음수의 간선이 존재할 경우 벨만-포트 알고리즘을 사용하면됩니다.
1. 다익스트라 알고리즘은 아직 확인되지않은 거리는 전부 초기값을 무한으로 잡습니다.
- Q 는 방문하지 않는 노드들의 집합

초기화를 실행합니다.
- 출발지를 A 로 설정했기 때문에 , d[A] = 0 이 된다. ( A 노드를 아직 방문한 것은 아니다)
- 출발지를 제외한 모든 노드들은 아직 확인되지 않았기에, d[다른 노드] = 무한이된다.
2. 루프를 돌려 이웃노드를 방문하고 거리를 계산한다.
- 노드 S (방문한 노드의 집합 및 최소 경로)

- 거리가 최소인 노드 N 을 방문하여 노드 N 과 연결된 모든 이웃 노드와의 거리를 측정하여 d[N] (출발지로부터 N 까지의 계산되 최소 거리값) + (N 과 이웃 노드간의 거리값) = 출발지부터 이웃노드까지의 거리값 이 계산된다. 새로 계산된 값이 기존에 저장된 값보다 작은 경우에만 d[N] 를 갱신한다.
- 초기화 직후의 첫 루프에서 시작 정점으로 부터의 거리가 최소인 노드는 A이므로 (A 자기 자신), 노드 A 를 방문하여 Q 에서 제거하고 S 에 추가하게 된다.
- 지금은 첫번째 루프만 끝난 상태로 단순히 0 + (이웃 노드와 출발지 사이의 거리값) = (출발지와 이웃 노드간의 거리값이) 이 각 이웃 노드까지의 거리값으로 기록된다.(무한보다 작기 때문에)
- 따라서, d[B] = 10, d[C] = 30, d[D] =15로 값을 갱신됩니다.
3. 첫 루프 이후의 그래프의 상태가 업데이트 되는 방식
- 두번째 루프를 마치고 난 뒤의 그래프
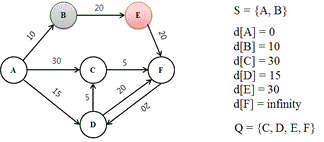
루프가 반복적으로 작동하는 방법을 설명합니다. 밑의 그림들 또한 루프안에서 알고리즘이 진행된느 순간들을 반복 설명합니다.
- 이전에 설명했듯이 , 방문할 노드 Q 에 남아있는 노드들 중 d[N] 값이 제일 작은것으로 선택된다. 따라서 Q = {B, C, D, E, F} 중 d[B] = 10 으로 제일 작은 값을 가지므로, B 를 방문하여 S 에서 추가하고 Q 에서 제거한다.
- 이제, B 의 이웃 노드들을 모두 탐색하여 거리를 재고 d[N] 에 기록한다. B 의 이웃 노드는 E 뿐이므로, d[E] 값이 무한에서 d[B] + (B로부터 E 까지의 거리값 20) = 30 으로 업데이트됩니다.
- 여기서 d[B] 값을 더하는 이유는 출발지로부터 해당 노드까지의 거리값을 재기 위해서이다.
4. 더 빠른 경로를 발견한 경우

- 세번째 루프에서 선택, 방문되는 노드는 D 이다. 두 번째 루프를 마친 후 Q 원소중에 제일 낮은 d[N] 값을 가진 것이 D 이기 때문이다. 따라서 루프를 마친 뒤인 S 에 D 가 추가되어 있는 것을 볼 수 있다.
- 이제 D 의 이웃 노드들 (C, F) 의 거리를 잰 후 d[N] 값을 업데이트한다. 이 때 d[C] 의 값은 A 를 방문할 때 이미 계산되어 30 으로 저장되어 있었으나, D 를 방문하여 C 와의 거리르 확인해 보니 20 으로 더 짧은 최단 경로가 발견되었다.
- 그러므로 d[c] 의 값을 30 -> 20 으로 변경한다.
- d[F] 의 경우에는 원래의 값이 무한이므로 , 더 작은 값인 15 + 20 = 35 로 변경한다.
5. 또 다른 반복 루프 상황
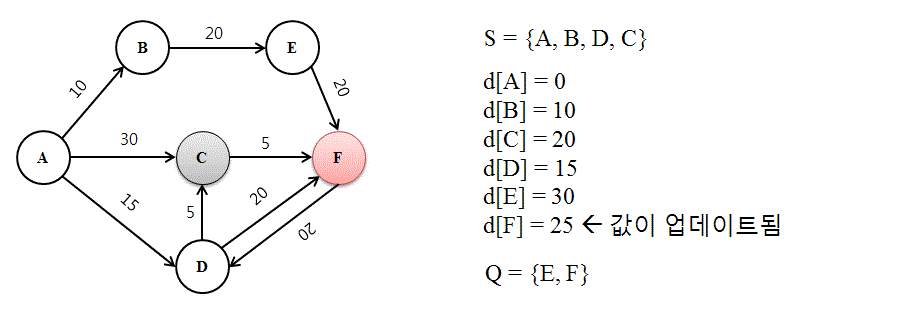
- Q = {C,E F} 증 d[C] = 20 으로 거리가 가장 짧은 C 를 방문하여, S 는 {A, B, D , C} 가 되었다.
- 다시 이웃노드와의 거리를 계산해보니, 이번에는 (A-> D) + (D + F) = 15 + 20 = 35 보다, (A-> D) + (D + C) + (C + F) = 15 + 5 + 5 = 25 로 더 작은 값을 가지는 것을 발견하였다. d[F] = 25 로 업데이트한다.
- 이 일련의 과정이 반복되어 Q 가 공집합이 되었다며, 남아있는 데이터로 추론하여 최단거리를 결정한다.
마지막 루프 이후
- S = {A , B, D, C, F, E}
- d[A]= 0
- d[B] = 10
- d[C] = 20
- d[D] = 15
- d[E] = 30
- d[F] = 25
- Q = ∅
A 부터 F 의 최단거리는 A-> D -> C -> F 가 최단 경로이며, 거리가 25 로 결정된다.
연관문제 :
- (프로그래머스) https://school.programmers.co.kr/learn/courses/30/lessons/72413
- (백준) https://www.acmicpc.net/problem/1753
'알고리즘' 카테고리의 다른 글
| 백준 16234 인구 이동 [JAVA] (1) | 2024.10.23 |
|---|---|
| 백준 11049 행렬 곱셈 순서 [JAVA] (2) | 2024.10.17 |
| 프로그래머스 광고삽입 [JAVA] (0) | 2024.10.02 |
| 프로그래머스 택배 배달과 수거하기 [JAVA] (2) | 2024.09.30 |
| 백준 2579 계단 오르기 [JAVA] (0) | 2024.09.30 |