공통부분 문자열
https://www.acmicpc.net/problem/5582
문제
두 문자열이 주어졌을 때, 두 문자열에 모두 포함된 가장 긴 공통 부분 문자열을 찾는 프로그램을 작성하시오.
어떤 문자열 s의 부분 문자열 t란, s에 t가 연속으로 나타나는 것을 말한다. 예를 들어, 문자열 ABRACADABRA의 부분 문자열은 ABRA, RAC, D, ACADABRA, ABRACADABRA, 빈 문자열 등이다. 하지만, ABRC, RAA, BA, K는 부분 문자열이 아니다.
두 문자열 ABRACADABRA와 ECADADABRBCRDARA의 공통 부분 문자열은 CA, CADA, ADABR, 빈 문자열 등이 있다. 이 중에서 가장 긴 공통 부분 문자열은 ADABR이며, 길이는 5이다. 또, 두 문자열이 UPWJCIRUCAXIIRGL와 SBQNYBSBZDFNEV인 경우에는 가장 긴 공통 부분 문자열은 빈 문자열이다.
입력
첫째 줄과 둘째 줄에 문자열이 주어진다. 문자열은 대문자로 구성되어 있으며, 길이는 1 이상 4000 이하이다.
출력
첫째 줄에 두 문자열에 모두 포함 된 부분 문자열 중 가장 긴 것의 길이를 출력한다.
예제 입력 1 복사
ABRACADABRA
ECADADABRBCRDARA
예제 출력 1 복사
5
두 문자열이 주어졌을 때 공통 문자열을 찾는 문제이다.
접근방법
모든 문자열의 경우를 구하여 비교하는 경우 시간초과가 발생하였다.
시간초과 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
class Main{
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String s1 = br.readLine();
String s2 = br.readLine();
int ans = 0;
for (int k = 1; k < s1.length(); k++) {
for (int i = 0; i+k <= s1.length(); i++) {
String substring = s1.substring(i, i + k);
if(s2.contains(substring)){
ans = substring.length();
}
}
}
System.out.println(ans);
}
}
큰 문제를 작은 문제로 나눠 생각할 수 있고 그 작은 문제들을 구한 해로 큰 문제의 값을 도출할 수 있다면 dp 문제로 풀어나갈 수 있을 것이다.
점화식을 도출해보자!
2차원 배열을 이용하여 두 문자열을 행, 열에 매칭합니다.
- 문자열 A , B 를 한글자씩 비교해봅시다.
- 두 문자가 다르다면 dp[i][j] 에 0 을 표시합니다.
- 같다면 dp[i-1][i-1] 값에 +1 을 합니다.
- 위 과정을 반복합니다.
이 과정의 성립이유는 공통 문자열은 연속되야 하기 때문입니다. 현재 두 문자가 같을 때 두 문자의 앞글자까지가 공통 문자열이라면 계속 공통 문자열이 이어질 것이고 아니라면 다시 본인 부터 공통 문자열을 만들어 가게 될것입니다.
- 앞마진이 0인 2차원 배열을 생성 , ABCDEF 문자열과 GBCDFE 문자열을 한 글자씩 비교한다.
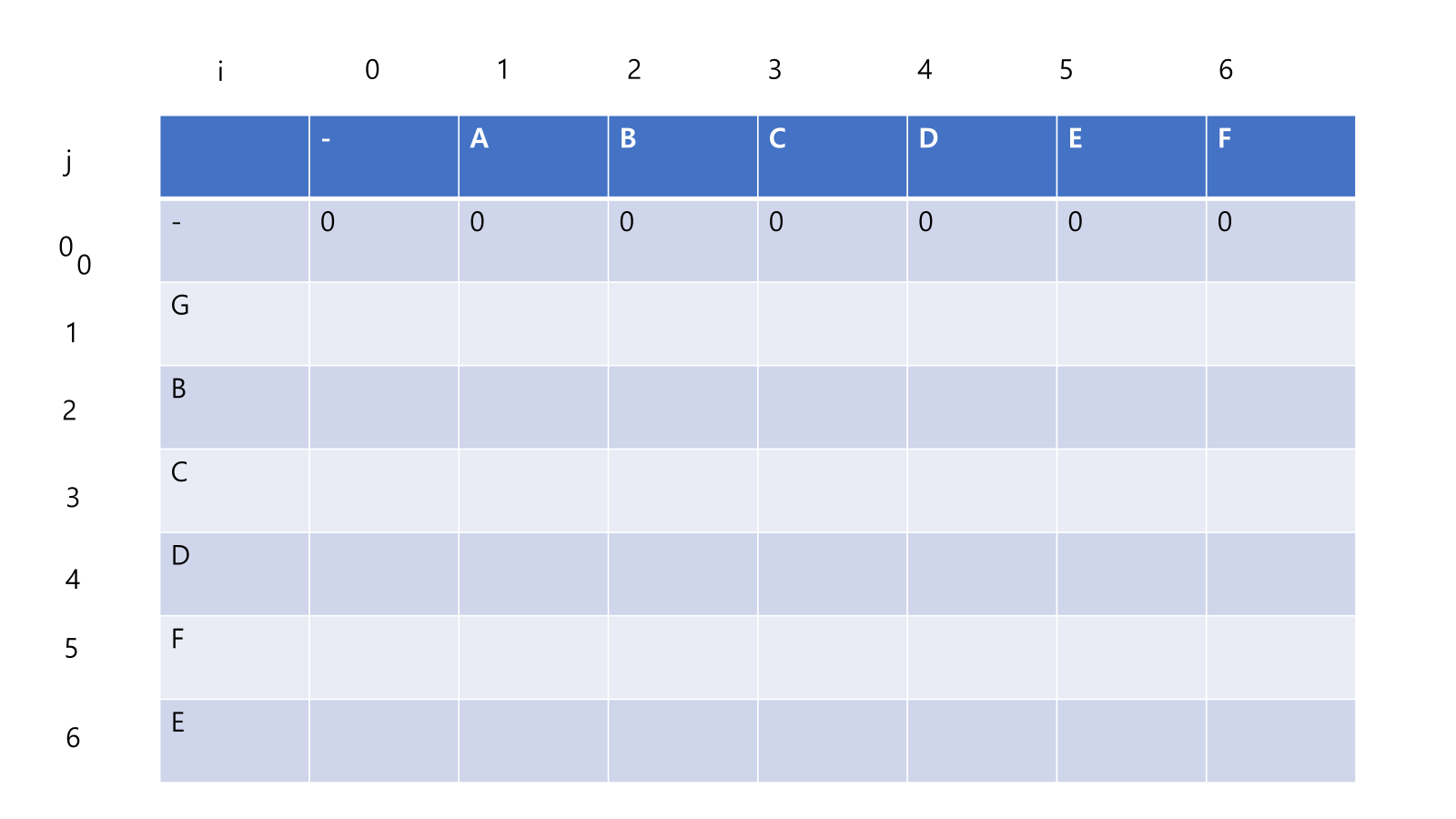
- G와 ABCDEF 와 한 글자씩 비교, 같은 문자가 없기 때문에 dp[i][j] 은 모두 0 으로 채워진다.

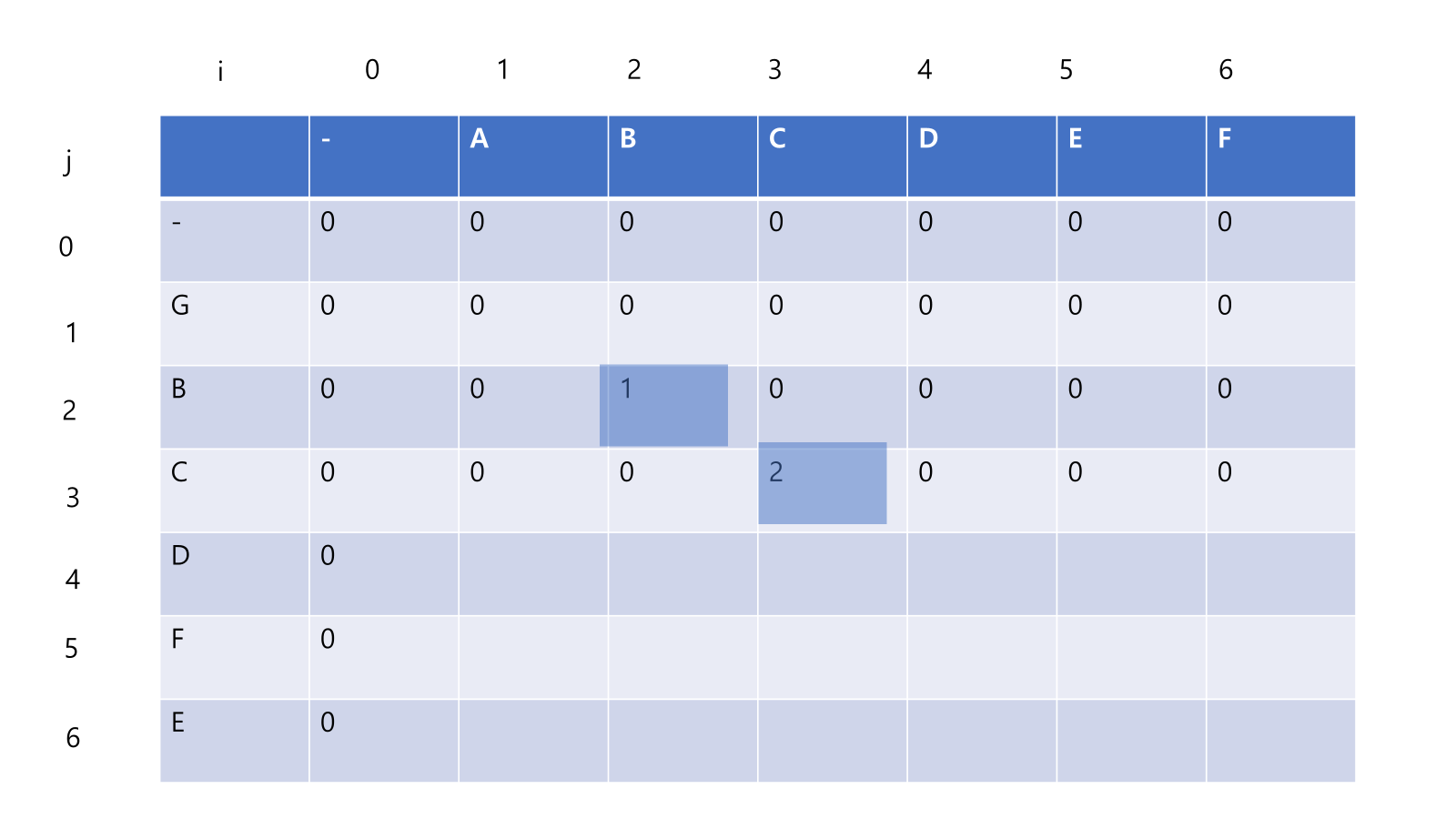
- 다음으로 B 를 ABCDEF 와 한 글자씩 비교, 같은 문자가 존재하면 dp[i][[j] = dp[i-1][[j-1] + 1;
- dp[2][2] = dp[1][1] + 1;
- 즉 AB GB 가 같으므로
- ABCDEF GBCDFE dp[1][1] 까지 비교한 값과 합해주는 것이다.

- 다음으로 C 를 ABCDEF 와 한글자씩 비교, 같은 문자가 존재하면 dp[i][[j] = dp[i-1][[j-1] + 1;
- dp[3][3] = dp[2][2] + 1;
- 즉 ABC GBC 가 같으므로
- AB GB dp[2][2] 까지 비교한 값과 합해주는 것이다.
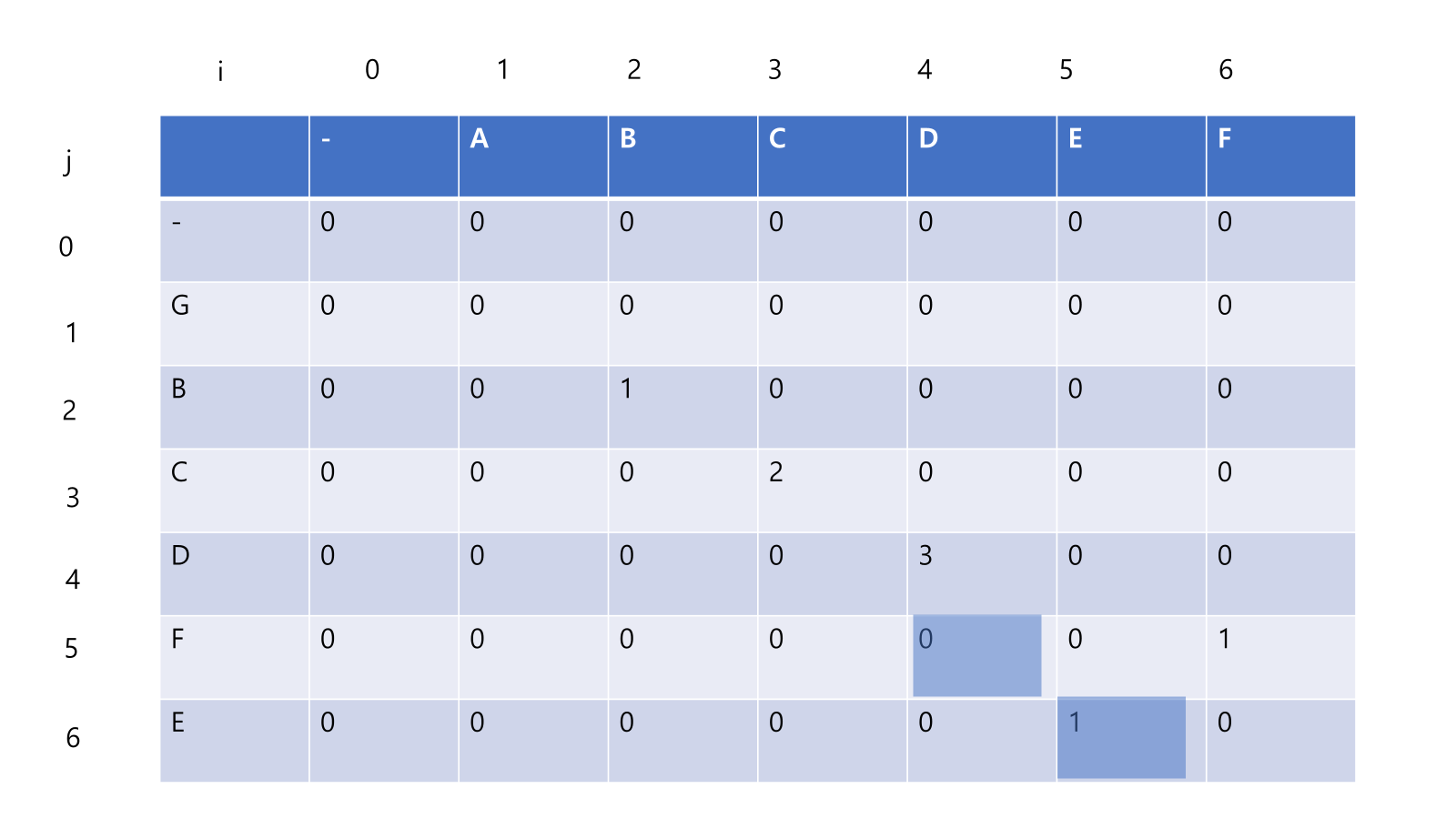
- 다음으로 D 를 ABCDEF 와 한글자씩 비교, 같은 문자가 존재하면 dp[i][[j] = dp[i-1][[j-1] + 1;
- dp[4][4] = dp[3][3] + 1;
- 즉 ABCD GBCD 가 같으므로
- ABC GBC dp[3][3] 까지 비교한 값과 합해주는 것이다.

-
- 다음으로 F 를 ABCDEF 와 한글자씩 비교, 같은 문자가 존재하면 dp[i][[j] = dp[i-1][[j-1] + 1;
- dp[5][6] = dp[4][5] + 1;
- 즉 ABCDEF GBCDF 가 같으므로
- ABCDE GBCD dp[5][4] 까지 비교한 값과 합해주는 것이다.

- 다음으로 E 를 ABCDEF 와 한글자씩 비교, 같은 문자가 존재하면 dp[i][[j] = dp[i-1][[j-1] + 1;
- dp[6][5] = dp[5][4] + 1;
- 즉 ABCDEF GBCDFE 가 같으므로
- ABCD GBCDF dp[5][4] 까지 비교한 값과 합해주는 것이다.
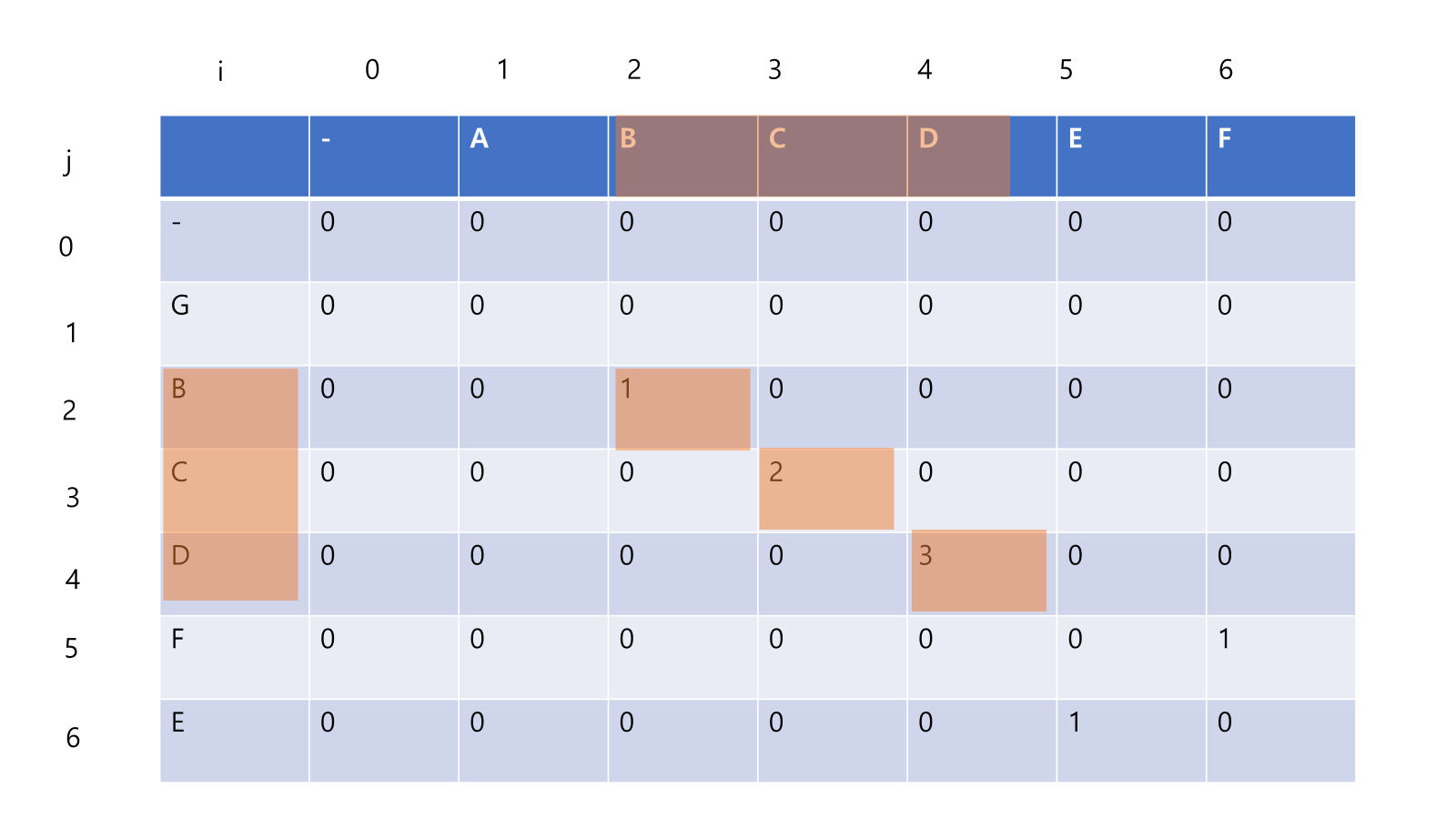
ABRACADABRA
ECADADABRBCRDARAimport java.io.BufferedReader;
import java.io.InputStreamReader;
class Main{
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String s1 = br.readLine();
String s2 = br.readLine();
int n = s1.length();
int m = s2.length();
int[][] dp = new int[n][m];
int max = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if(s1.charAt(i) == s2.charAt(j)) {
if(i-1 < 0 || j -1 < 0) {
dp[i][j] = 1;
max = Math.max(max, dp[i][j]);
} else {
dp[i][j] = dp[i-1][j-1] + 1;
max = Math.max(max, dp[i][j]);
}
}
}
}
System.out.println(max);
}
}
참고자료:
'알고리즘' 카테고리의 다른 글
| Java 저울 백준 - 2437 (1) | 2025.02.19 |
|---|---|
| 백준 12886 돌 그룹 [JAVA] (1) | 2024.10.31 |
| 백준 16928 뱀과 사다리 게임 [JAVA] (1) | 2024.10.26 |
| 백준 16234 인구 이동 [JAVA] (1) | 2024.10.23 |
| 백준 11049 행렬 곱셈 순서 [JAVA] (2) | 2024.10.17 |